Question!
Write a program that simulates a (single) checkout line at a supermarket. The line is a queue object. Customer(i.e., customer objects) arrive in random integer intervals of 1—4 minutes. Also, each customer is served in random integer intervals of 1—4 minutes. Run the supermarket simulation for a 12-hour day (720 minutes) using the following algorithm:
For the better service at the next time, the supermarket decided to record the name of the customers. A customer’s name is a random integer between 0 to 10000. Whenever a new customer arrives at the queue, you assign a new random name to the customer. We assume the customer’s name is unique for every customer. For efficiency, the customers’ names are recorded in the binary search tree structure (forget about balancing).
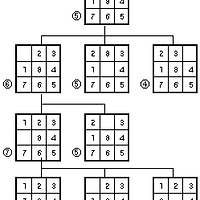
After the simulation, you display the binary tree for the customers’ names on the screen. The function should output the tree row by row, with the top of the tree at the left on the screen and the bottom of the tree toward the right of the screen. Each row is output vertically. For example, one example output is as follows:
where 83 is a root of the tree having left child 71 and right child 97, and so on.
Solution!
1) Description the usage of the program.
1-1) Execution * At the Console Window, Use a similar form following. And there are two execution way.
① First Way : If you just input the command ‘simulate’, You can simulate the program with default value. - Default Value 1: Maximum Interval time of customers’ arrival is 4 (1 ~ 4 minutes) - Default Value 2: Maximum Interval time of service for customer is 4 (1 ~ 4 minutes) - Default Value 3: Simulation Time : 720 minutes
② Second Way : You can add the extra parameters like the following example
- First extra parameter: You can set the maximum interval time of customers’ arrival - Second extra parameter: You can set the maximum interval time of service for customer - Third extra parameter: You can set the simulation time
* Notice : If you just only input one or two additional parameters, the parameters are not applied to program. So this program is executed with default values
1-2) Execution Result
* You can see the following result after execution
It shows the number of customers in the line at every time, (This data amount is so large, So you can’t see the all data)
And the ‘in’ and ‘out’ marks mean that customers in and out at the checkout line.
It shows the maximum number of customers in the queue at particular time and longest wait time of particular customer among all customers.
It shows the binary search tree of customers’ names to 5 levels of the name tree from the root.
* Another Example (Execution command : simulate 4 4 720)
2) Implementation
2-1) Queue
l I implemented the Queue structure using double linked list. The queue in this program consist of queue node structure, some additional variables and some functions(Enqueue, Dequeue and so on).
|
Implemented Part |
Location |
Description |
|
Queue Node Structure |
20 ~ 25 Line |
It is used to save one node in queue |
|
Head and Tail Node |
36 Line |
It is the head and tail node for double linked list, that is to say, head node means ‘front’ and tail node means ‘rear’ in queue concept. |
|
Variables for queue |
37 ~ 40 Line |
It is used to solve the problem about queue in spec. |
|
Functions for queue |
48 ~ 52 Line |
There is functions’ declaration for queue operation |
|
InitQueue() |
151~161 Line |
Initialize the queue |
|
Enqueue(int value) |
164~183 Line |
Put data to rear of queue |
|
Dequeue() |
186~205 Line |
Get data from front of queue |
|
ClearQueue() |
208~233 Line |
Release all queue data. Namely, Initialize the queue |
|
AddWaitTimeToQueue() |
226~236 Line |
Add the waiting time at the line per customer (Extra function) |
2-2) Binary Search Tree
l The tree in this program consist of tree node structure, some additional variables and some functions(InsertToTree, OutputTree and so on)
Implemented Part Location Description Tree Node Structure 28 ~ 33 Line It is used to save one node in tree Base Node 43 Line It is the base node of tree Variables for queue 44 ~ 45 Line It is used to solve the problem about binary search tree in spec. Functions for queue 55 ~ 58 Line There is functions’ declaration for tree operation InitTree(int initValue) 242~248 Line Initialize binary search tree InsertToTree(int value) 251~280 Line Insert data to proper position of tree GetNewCustomerNumber() 283~300 Line Get new customer's name without overlapping (Extra function) OutputTree(tnode *node, int totalSpace, int depth) 307~326 Line Output the tree on screen
3)Test Cases
3-1) What is the maximum number of customers in the queue at any time?
* To solve this problem, I makes two additional variables – maxNumber, maxTime
> maxNumber : this variable always maintain the maximum number of customers in queue
> maxTime : maxTime save that time when maxNumber variable is updated
* And every time when 1 minute passes, I checked the number of customers in queue. So if the number of customers in current-state queue is larger than maxNumber, change the maxNumber data as number of customers in current-state queue. So the maxNumber always can maintain the maximum number of customers in the queue at particular time
* Please, refer the 101~105 Lines in source code.
3-2) What is the longest wait any one customer experiences?
* To solve this problem, I save the customer’s waiting time in the each queue node (waitTime) and maxWaitTime.
> maxWaitTime: this variable always maintain the longest wait time of particular customer among all customers.
First, customer comes to the checkout line, Input the customer data to queue, and initialize the customers’ wait time to 0. And Whenever 1 minute passes, add 1 minute to the each customers’ wait time. And if a customer get out from the checkout line (Dequeue operation), Compare the value with maxWaitTime. So if the current customer’s wait time is larger than maxWaitTime, change the maxWaitTime data as the current customer’s wait time.
* Please, refer the 122~128 Lines in source code.
3-3) What happens if the arrival interval is changed from 1—4 minutes to 1—3 minutes?
* These are some examples that the arrival interval is changed to 1-3 minutes
* As you can see, If the arrival interval is changed from 1 – 4 minutes to 1 – 3 minutes, Generally, the maximum number of customers and longest wait time is getting lager than data of general case.
* The reason: ‘The arrival interval time is getting smaller’ means ‘the many more customers can come to the checkout line’. Because the arrival interval time is small, the queue maybe take more customers. But the service interval time is not decreased. So the same service time is needed as ever.
* Result : The number of customers that comes in checkout line is increased and the processing time of service for customers is same. In result the queue is larger and the processing efficiency will be slower.
'개발&컴퓨터 > 알고리즘' 카테고리의 다른 글
| [알고리즘문제] 문자열 정렬하기 (0) | 2016.05.17 |
|---|---|
| Search in Artificial Intelligence (기초) (0) | 2016.02.29 |
| Convex Hull Problem (Clustering Algorithm) (0) | 2015.10.11 |
| Cellular Automata 를 이용한 Forest Fire Modeling 구현 (2) (0) | 2015.09.12 |
| Cellular Automata 를 이용한 Forest Fire Modeling (1) (0) | 2015.09.07 |










 supermarket_simulation.zip
supermarket_simulation.zip